Given Position Function Find Total Distance Traveled

4.1: Determining Distance Traveled from Velocity

1. Last updated

2. Salvage as PDF

Folio ID

4313

• 
• 1000 Valley Land University via ScholarWorks @Grand Valley State University

Learning Objectives

In this section, we strive to sympathize the ideas generated by the following important questions:

• If we know the velocity of a moving body at every point in a given interval, can we make up one's mind the distance the object has traveled on the time interval?
• How is the problem of finding distance traveled related to finding the area under a certain bend?
• What does it mean to antidifferentiate a role and why is this process relevant to finding distance traveled?
• If velocity is negative, how does this bear on the problem of finding distance traveled?

In the very offset department of the text, nosotros considered a situation where a moving object had a known position at time t. In item, we stipulated that a tennis brawl tossed into the air had its elevation southward (in anxiety) at fourth dimension t (in seconds) given by southward(t) = 64 − sixteen(t − 1) ii . From this starting point, we investigated the average velocity of the ball on a given interval [a, b], computed by the difference quotient southward(b)−s(a) b−a , and eventually institute that we could determine the exact instantaneous velocity of the ball at time t by taking the derivative of 207 208 the position function, s 0 (t) = lim h→0 s(t + h) − s(t) h . Thus, given a differentiable position function, we are able to know the exact velocity of the moving object at any point in time. Moreover, from this foundational problem involving position and velocity we have learned a groovy bargain. Given a differentiable office f , we are now able to find its derivative and apply this derivative to make up one's mind the function'south instantaneous rate of change at whatsoever point in the domain, as well every bit to find where the function is increasing or decreasing, is concave up or concave down, and has relative extremes. The vast majority of the bug and applications we have considered take involved the situation where a particular function is known and we seek information that relies on knowing the function'due south instantaneous rate of change. That is, we accept typically proceeded from a function f to its derivative, f 0 , and so used the pregnant of the derivative to assist usa answer important questions. In a much smaller number of situations so far, we have encountered the reverse situation where we instead know the derivative, f 0 , and have tried to deduce information about f . Information technology is this particular trouble that will exist the focus of our attention in most of Chapter 4: if we know the instantaneous rate of change of a office, are we able to make up one's mind the function itself? To begin, we kickoff with a more than focused question: if we know the instantaneous velocity of an object moving along a straight line path, tin we decide its respective position function?

Preview Activity \(\PageIndex{ane}\):

Suppose that a person is taking a walk along a long direct path and walks at a constant rate of 3 miles per hour.

Figure iv.1: At left, axes for plotting y = v(t); at right, for plotting y = s(t).

1. On the left-mitt axes provided in Effigy 4.1, sketch a labeled graph of the velocity part v(t) = 3. Notation that while the calibration on the ii sets of axes is the same, the units on the right-hand axes differ from those on the left. The correct-hand axes 209 will exist used in question (d).
2. How far did the person travel during the two hours? How is this distance related to the surface area of a certain region under the graph of y = v(t)?
3. Find an algebraic formula, s(t), for the position of the person at time t, assuming that s(0) = 0. Explain your thinking.
4. On the correct-mitt axes provided in Figure 4.1, sketch a labeled graph of the position role y = s(t).
5. For what values of t is the position function s increasing? Explicate why this is the instance using relevant information about the velocity function v.

Area under the graph of the velocity function In Preview Action 4.1, we encountered a central fact: when a moving object's velocity is abiding (and positive), the expanse under the velocity curve over a given interval tells us the altitude the object traveled. Equally seen at left in Effigy 4.2, if we consider an object

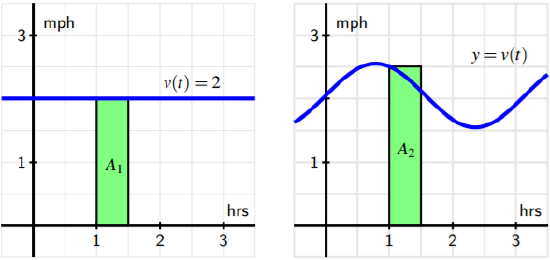
Effigy 4.two: At left, a constant velocity function; at right, a non-constant velocity function.

moving at 2 miles per hour over the fourth dimension interval [1, one.5], then the area A1 of the shaded region under y = v(t) on [ane, ane.5] is A1 = 2 miles hr · one 2 hours = 1 mile. This principle holds in general simply due to the fact that altitude equals charge per unit times time, provided the charge per unit is constant. Thus, if v(t) is constant on the interval [a, b], then the 210 altitude traveled on [a, b] is the surface area A that is given by A = v(a)(b − a) = v(a)4t, where 4t is the change in t over the interval. Notation, too, that nosotros could utilise any value of five(t) on the interval [a, b], since the velocity is constant; we simply chose v(a), the value at the interval's left endpoint. For several examples where the velocity function is piecewise constant, see http://gvsu.edu/s/9T. 1 The situation is obviously more complicated when the velocity role is non abiding. At the same time, on relatively small intervals on which five(t) does not vary much, the surface area principle allows united states of america to estimate the distance the moving object travels on that time interval. For instance, for the non-constant velocity function shown at right in Figure 4.2, we see that on the interval [one, 1.v], velocity varies from v(1) = 2.5 down to v(1.5) ≈ 2.1. Hence, 1 estimate for altitude traveled is the area of the pictured rectangle, A2 = 5(1)4t = 2.5 miles hour · i ii hours = 1.25 miles. Because v is decreasing on [1, 1.five] and the rectangle lies higher up the curve, clearly A2 = 1.25 is an over-estimate of the actual distance traveled. If nosotros desire to judge the surface area under the non-constant velocity function on a wider interval, say [0, 3], it becomes credible that one rectangle probably will not give a good approximation. Instead, we could employ the half-dozen rectangles pictured in Figure iv.3, find the

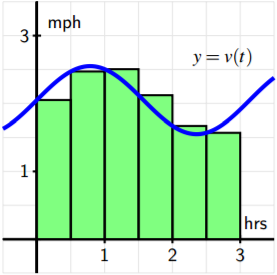
Figure iv.3: Using six rectangles to estimate the area nether y = v(t) on [0, 3].

area of each rectangle, and add together up the total. Apparently there are choices to make and problems to understand: how many rectangles should nosotros use? where should we evaluate the function to determine the rectangle's height? what happens if velocity is sometimes negative? 1Marc Renault, calculus applets. 211 can we attain the exact area under any non-abiding curve? These questions and more are ones we will study in what follows; for at present it suffices to realize that the simple idea of the area of a rectangle gives united states a powerful tool for estimating both distance traveled from a velocity function as well as the area under an arbitrary curve. To explore the setting of multiple rectangles to approximate area under a not-constant velocity function, encounter the applet found at http://gvsu.edu/s/9U. 2

Action \(\PageIndex{2}\):

Suppose that a person is walking in such a fashion that her velocity varies slightly according to the information given in the table beneath and graph given in Effigy 4.iv.

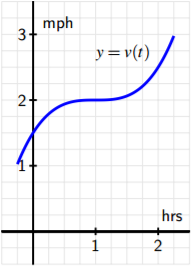
Effigy 4.4: The graph of y = five(t).2Marc Renault, calculus applets. 212

1. Using the grid, graph, and given data appropriately, estimate the distance traveled by the walker during the two hr interval from t = 0 to t = 2. You should utilise time intervals of width 4t = 0.five, choosing a manner to use the function consistently to determine the peak of each rectangle in order to approximate distance traveled.
2. How could you lot get a better approximation of the distance traveled on [0, 2]? Explain, and so observe this new estimate.
3. At present suppose that you lot know that v is given past five(t) = 0.5t 3 − i.5t 2 + i.5t + 1.5. Remember that v is the derivative of the walker's position office, s. Observe a formula for s then that due south 0 = five.
4. Based on your piece of work in (c), what is the value of s(2)− s(0)? What is the significant of this quantity?

Two approaches: Surface area and Antidifferentiation

When the velocity of a moving object is positive, the object'southward position is always increasing. While we will soon consider situations where velocity is negative and think almost the ramifications of this status on altitude traveled, for now we continue to presume that we are working with a positive velocity office. In that setting, nosotros have established that whenever 5 is actually abiding, the exact distance traveled on an interval is the area under the velocity curve; furthermore, we have observed that when v is not constant, we tin estimate the total distance traveled by finding the areas of rectangles that help to approximate the area under the velocity bend on the given interval. Hence, we see the importance of the problem of finding the area between a bend and the horizontal axis: besides beingness an interesting geometric question, in the setting of the curve being the (positive) velocity of a moving object, the expanse under the curve over an interval tells united states the exact distance traveled on the interval. We can approximate this expanse whatever fourth dimension nosotros accept a graph of the velocity function or a table of data that tells us some relevant values of the function. In Activity 4.1, we also encountered an alternate arroyo to finding the altitude traveled. In item, if nosotros know a formula for the instantaneous velocity, y = v(t), of the moving body at time t, then we realize that v must be the derivative of some corresponding position role s. If we tin can find a formula for s from the formula for five, it follows that we know the position of the object at time t. In add-on, under the assumption that velocity is positive, the change in position over a given interval then tells us the distance traveled on that interval. For a elementary example, consider the situation from Preview Activity 4.1, where a person is walking along a straight line and has velocity function v(t) = 3 mph. As pictured in

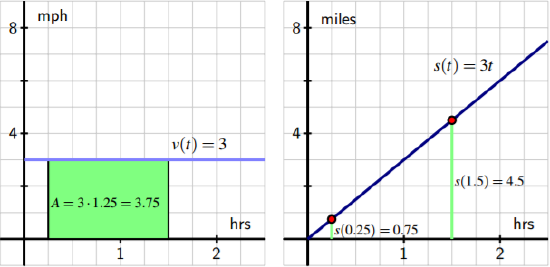
Effigy 4.v: The velocity function five(t) = three and corresponding position function s(t) = 3t.

Figure 4.5, we come across the already noted relationship betwixt area and distance traveled on the left-hand graph of the velocity function. In improver, because the velocity is constant 213 at iii, we know that if3 south(t) = 3t, so s 0 (t) = three, so s(t) = 3t is a function whose derivative is v(t). Furthermore, we now observe that s(ane.5) = four.5 and s(0.25) = 0.75, which are the respective locations of the person at times t = 0.25 and t = 1.5, and therefore due south(1.five) − south(0.25) = 4.v − 0.75 = 3.75 miles. This is non only the change in position on [0.25, 1.5], simply also precisely the distance traveled on [0.25, one.five], which tin also be computed by finding the area nether the velocity curve over the aforementioned interval. At that place are profound ideas and connections nowadays in this instance that we will spend much of the remainder of Affiliate 4 studying and exploring. For now, it is most important to observe that if nosotros are given a formula for a velocity part 5, it tin exist very helpful to detect a office south that satisfies due south 0 = v. In this context, we say that s is an antiderivative of five. More mostly, just equally we say that f 0 is the derivative of f for a given part f , if we are given a role g and Yard is a function such that G 0 = chiliad, we say that G is an antiderivative of thousand. For example, if 1000(x) = 3x 2 + 2x, an antiderivative of k is Yard(x) = ten three + x ii , since G 0 (10) = g(x). Annotation that we say "an" antiderivative of g rather than "the" antiderivative of g because H(x) = x iii + x 2 + 5 is also a function whose derivative is chiliad, and thus H is another antiderivative of g.

Activity \(\PageIndex{3}\):

A ball is tossed vertically in such a style that its velocity function is given by v(t) = 32 − 32t, where t is measured in seconds and 5 in feet per second. Assume that this part is valid for 0 ≤ t ≤ 2.

1. For what values of t is the velocity of the ball positive? What does this tell you about the motion of the ball on this interval of time values?
2. Notice an antiderivative, southward, of five that satisfies due south(0) = 0.
3. Compute the value of s(1) − southward( 1 2 ). What is the meaning of the value yous find?
4. Using the graph of y = v(t) provided in Figure 4.six, detect the exact area of the region under the velocity curve between t = ane 2 and t = 1. What is the pregnant of the value you find?
5. Answer the aforementioned questions as in (c) and (d) but instead using the interval [0, 1]. (f) What is the value of s(2) − s(0)? What does this issue tell you about the flight of the ball? How is this value connected to the provided graph of y = 5(t)? Explain. C

Hither we are making the implicit supposition that southward(0) = 0; nosotros will further hash out the dissimilar possibilities for values of southward(0) in subsequent study.

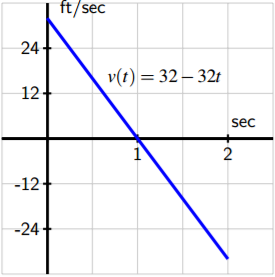
Figure four.6: The graph of y = v(t).

When velocity is negative Most of our work in this section has occurred under the assumption that velocity is positive. This hypothesis guarantees that the movement of the object under consideration is ever in a single direction, and hence ensures that the moving trunk'due south change in position is the same as the distance it travels on a given interval. As we saw in Activity four.2, there are natural settings in which a moving object'southward velocity is negative; we would like to understand this scenario fully as well. Consider a uncomplicated example where a person goes for a walk on a beach along a stretch of very straight shoreline that runs east-westward. We tin can naturally presume that their initial position is s(0) = 0, and further stipulate that their position function increases as they move e from their starting location. For case, a position of s = i mile represents being 1 mile east of the start location, while s = −1 tells us the person is one mile westward of where they began walking on the beach. At present suppose the person walks in the following manner. From the starting time at t = 0, the person walks due east at a constant rate of iii mph for 1.5 hours. After 1.5 hours, the person stops abruptly and begins walking due westward at the constant charge per unit of 4 mph and does and so for 0.five hours. Then, later another abrupt cease and start, the person resumes walking at a abiding charge per unit of 3 mph to the east for i more hour. What is the total distance the person traveled on the time interval t = 0 to t = 3? What is the person'southward total change in position over that time? On one hand, these are simple questions to answer considering the velocity involved is constant on each interval. From t = 0 to t = ane.5, the person traveled D[0,ane.5] = three miles per hour · i.5 hours = four.five miles. Similarly, on t = one.v to t = 2, having a different rate, the altitude traveled is D[one.v,ii] = 4 miles per hour · 0.5 hours = 2 miles. 215 Finally, similar calculations reveal that in the last hr, the person walked D[two,three] = 3 miles per 60 minutes · ane hours = 3 miles, so the total distance traveled is D = D[0,1.5] + D[one.five,2] + D[2,3] = 4.5 + 2 + iii = ix.5 miles. Since the velocity on 1.5 < t < two is actually v = −iv, being negative to point motion in the westward direction, this tells the states that the person first walked 4.5 miles east, and then ii miles west, followed by 3 more miles east. Thus, the walker'southward total change in position is alter in position = 4.5 − two + iii = v.5 miles. While we have been able to answer these questions fairly easily, it is likewise important to think about this problem graphically in society that we can generalize our solution to the more complicated setting when velocity is not constant, besides as to note the item impact that negative velocity has. In Figure four.vii, we see how the distances we computed

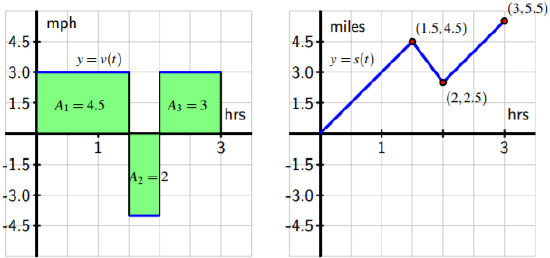
Figure iv.seven: At left, the velocity function of the person walking; at right, the respective position role.

higher up can be viewed as areas: A1 = four.5 comes from taking charge per unit times fourth dimension (3 · one.five), as practice A2 and A3 for the second and third rectangles. The big new issue is that while A2 is an area (and is therefore positive), because this expanse involves an interval on which the velocity function is negative, its area has a negative sign associated with it. This helps us to distinguish between distance traveled and modify in position. The distance traveled is the sum of the areas, D = A1 + A2 + A3 = iv.v + 2 + iii = ix.5 miles. 216 Simply the change in position has to business relationship for the sign associated with the surface area, where those in a higher place the t-centrality are considered positive while those beneath the t-axis are viewed as negative, so that due south(three) − southward(0) = (+iv.v) + (−2) + (+3) = 5.five miles, assigning the "−two" to the expanse in the interval [1.5, two] considering there velocity is negative and the person is walking in the "negative" direction. In other words, the person walks 4.5 miles in the positive direction, followed by two miles in the negative direction, and then three more miles in the positive management. This affect of velocity beingness negative is also seen in the graph of the function y = southward(t), which has a negative gradient (specifically, its slope is −4) on the interval 1.5 < t < two since the velocity is −4 on that interval, which shows the person'south position office is decreasing due to the fact that she is walking east, rather than w. On the intervals where she is walking west, the velocity function is positive and the slope of the position function s is therefore besides positive. To summarize, we run across that if velocity is sometimes negative, this makes the moving object's change in position different from its distance traveled. By viewing the intervals on which velocity is positive and negative separately, we may compute the distance traveled on each such interval, and and then depending on whether nosotros desire total altitude traveled or total alter in position, we may account for negative velocities that account for negative change in position, while withal contributing positively to total distance traveled. We close this section with ane additional activity that farther explores the effects of negative velocity on the problem of finding modify in position and total distance traveled.

Activity \(\PageIndex{4}\):

Suppose that an object moving along a directly line path has its velocity v (in meters per 2nd) at time t (in seconds) given by the piecewise linear office whose graph is pictured in Figure four.8. We view movement to the right equally being in the positive direction (with positive velocity), while movement to the left is in the negative direction. Suppose

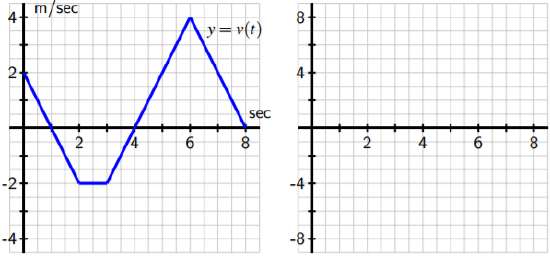
Figure four.viii: The velocity office of a moving object.

farther that the object's initial position at fourth dimension t = 0 is s(0) = 1.

1. Make up one's mind the total distance traveled and the total alter in position on the time interval 0 ≤ t ≤ ii. What is the object'due south position at t = 2?
2. On what time intervals is the moving object'due south position office increasing? Why? On what intervals is the object's position decreasing? Why?
3. What is the object'southward position at t = 8? How many total meters has it traveled to get to this point (including altitude in both directions)? Is this unlike from the object'due south total change in position on t = 0 to t = 8?
4. Find the exact position of the object at t = 1, ii, 3, . . ., 8 and use this information to sketch an accurate graph of y = due south(t) on the axes provided at right. How tin you use the provided information nearly y = v(t) to determine the concavity of s on each relevant interval?

Summary

In this section, we encountered the following important ideas:

• If nosotros know the velocity of a moving torso at every point in a given interval and the velocity is positive throughout, we tin can estimate the object'south distance traveled and in some circumstances decide this value exactly.
• In particular, when velocity is positive on an interval, we can discover the total altitude traveled by finding the area under the velocity curve and above the t-axis on the given time interval. We may only be able to estimate this area, depending on the shape of the velocity curve.
• An antiderivative of a function f is a new function F whose derivative is f . That is, F is an antiderivative of f provided that F 0 = f . In the context of velocity and position, if we know a velocity function v, an antiderivative of v is a position part s that satisfies s 0 = five. If v is positive on a given interval, say [a, b], and so the change in position, s(b) − s(a), measures the distance the moving object traveled on [a, b].
• In the setting where velocity is sometimes negative, this means that the object is sometimes traveling in the opposite direction (depending on whether velocity is positive or negative), and thus involves the object backtracking. To determine distance traveled, we have to remember about the problem separately on intervals where velocity is positive and negative and business relationship for the change in position on each such interval.

Share this post